[イラレ]
Illustrator Script: Move to the right in proportion to the distance from the left end.
ご要望があったので、昔公開したスクリプトを1つ英訳しました。
You can run this script when multiple items or one group are selected in Illustrator CS6 or later.
Move the slider to move each selected item to the right by a distance proportional to the distance from the left end of the selected items.
[Download]
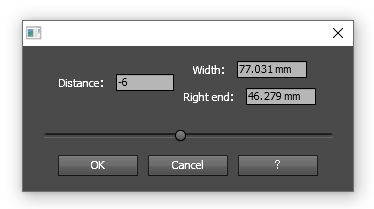
Distance : Moving distance (Original distance from the left end = 100)
Width : Overall width of selected items
Right end : X coordinate of the right end
You can run this script when multiple items or one group are selected in Illustrator CS6 or later.
Move the slider to move each selected item to the right by a distance proportional to the distance from the left end of the selected items.
[Download]
About dialog
Distance : Moving distance (Original distance from the left end = 100)
Width : Overall width of selected items
Right end : X coordinate of the right end
Movie
左端からの距離に比例した移動量で動かすやつ(イラレスクリプト) pic.twitter.com/A1l6YRhbV8
— あるふぁ(仮) (@peprintenpa) 2018年11月8日
PR
[イラレ]
イラレスクリプトで特定の座標を中心にした回転
イラレスクリプトの座標系は、右がx軸の+方向、上がy軸の+方向で、原点はアートボードを特に動かしてなければ1つ目のアートボード左上になります。単位はpt。
なので座標 (100,100) はこのあたり。

で、今回はこの (100,100) を中心に選択アイテムを30°回転するというスクリプトを書いてみようという話です。
ページアイテムを回転するメソッドといえば rotate ですが、これは6番目の引数で回転の中心を指定できます。選べるのは以下の10個。
Transformation.DOCUMENTORIGIN
Transformation.TOPLEFT
Transformation.LEFT
Transformation.BOTTOMLEFT
Transformation.TOP
Transformation.CENTER
Transformation.BOTTOM
Transformation.TOPRIGHT
Transformation.RIGHT
Transformation.BOTTOMRIGHT
残念ながら中心の座標を数値で指定する選択肢はありません。
しかしDOCUMENTORIGIN、つまり座標でいえば (0,0) なら選ぶことができます。
そこでこう考えます。
(-100,-100) ほど移動
↓
(0,0) を中心に30°回転
↓
(+100,+100) ほど移動
をすれば、点 (100,100) を中心に30°回転したのと同じじゃん!と。
移動のメソッドtranslateと回転のメソッドrotateを使えば次のように書くことができます。
これでできあがり、でもいいんですが、
なんかアイテム1つにつき移動→回転→移動と3つもメソッド使ってると、大量のアイテムを処理するとき重くなるかもしれないし、なんかもうちょっと良い書き方はないかしら、と考えてみます。
イラレのPageItemには transform というメソッドがあります。
これはTransformationMatrix(変形行列、2次元アフィン行列)という、次式のような6つの変数を持つ行列を使って変形を行うものです。

ここでいう変形とは、回転、移動、拡大縮小(縦横比を保持しないものも含む)、シアー、およびそれらの組み合わせです。
たとえば「原点を中心にθ回転」の変形行列は

となります。
ある点(x,y)を「原点を中心にθ回転」した点(x',y')は、行列とベクトルの掛け算を使って、

で求めることができます。
しかし、こんな式は覚えなくても大丈夫です。
Illustratorスクリプトには便利な組み込み関数があって、
getRotationMatrix で回転の変形行列
getTranslationMatrix で移動の変形行列
を得ることができます。getRotationMatrixの引数は普通の角度でOKです。ラジアンを使う必要もありません。
これらを使って上記スクリプトを書き換えると…
うーん、これでは何も改善してませんね。
点(x,y)を表すベクトルをrとして、
(-100,-100)移動の変形行列をA、原点を中心に30°回転の変形行列をB、(+100,+100)移動の変形行列をCとしたとき、
rを(-100,-100)移動した点は
Ar
rを(-100,-100)移動して、原点を中心に30°回転した点は
B(Ar)
rを(-100,-100)移動して、原点を中心に30°回転して、さらに(+100,+100)移動した点は
C(B(Ar))
で表せます。
そして、行列の掛け算はなんと、結合則が使えるのです!
すなわち、
C(B(Ar)) = (CBA)r
これは事前にCとBとAを掛け算した変形行列を求めておけば、変形1回で「(-100,-100)移動して、原点を中心に30°回転して、さらに(+100,+100)移動」したのと同じ状態にできる、ということです。
んで、イラレはその変形行列の掛け算にも関数を用意してくれています。concatenateMatrixというやつです。
なんか上はごちゃごちゃしましたけど、forループがシンプルになったので今度こそできあがりでーす。
ちなみにconcatenateTranslationMatrixとかconcatenateRotationMatrixとか使うともう少し短く書くこともできます。詳しくはOMビューワとかこことか見てください。
おしモアイ
なので座標 (100,100) はこのあたり。
で、今回はこの (100,100) を中心に選択アイテムを30°回転するというスクリプトを書いてみようという話です。
ページアイテムを回転するメソッドといえば rotate ですが、これは6番目の引数で回転の中心を指定できます。選べるのは以下の10個。
Transformation.DOCUMENTORIGIN
Transformation.TOPLEFT
Transformation.LEFT
Transformation.BOTTOMLEFT
Transformation.TOP
Transformation.CENTER
Transformation.BOTTOM
Transformation.TOPRIGHT
Transformation.RIGHT
Transformation.BOTTOMRIGHT
残念ながら中心の座標を数値で指定する選択肢はありません。
しかしDOCUMENTORIGIN、つまり座標でいえば (0,0) なら選ぶことができます。
そこでこう考えます。
(-100,-100) ほど移動
↓
(0,0) を中心に30°回転
↓
(+100,+100) ほど移動
をすれば、点 (100,100) を中心に30°回転したのと同じじゃん!と。
移動のメソッドtranslateと回転のメソッドrotateを使えば次のように書くことができます。
var sel=app.activeDocument.selection;
for(var i=0;i<sel.length;i++){
sel[i].translate(-100,-100);
sel[i].rotate(30,true,true,true,true,Transformation.DOCUMENTORIGIN);
sel[i].translate(100,100);
}これでできあがり、でもいいんですが、
なんかアイテム1つにつき移動→回転→移動と3つもメソッド使ってると、大量のアイテムを処理するとき重くなるかもしれないし、なんかもうちょっと良い書き方はないかしら、と考えてみます。
イラレのPageItemには transform というメソッドがあります。
これはTransformationMatrix(変形行列、2次元アフィン行列)という、次式のような6つの変数を持つ行列を使って変形を行うものです。
ここでいう変形とは、回転、移動、拡大縮小(縦横比を保持しないものも含む)、シアー、およびそれらの組み合わせです。
たとえば「原点を中心にθ回転」の変形行列は
となります。
ある点(x,y)を「原点を中心にθ回転」した点(x',y')は、行列とベクトルの掛け算を使って、
で求めることができます。
しかし、こんな式は覚えなくても大丈夫です。
Illustratorスクリプトには便利な組み込み関数があって、
getRotationMatrix で回転の変形行列
getTranslationMatrix で移動の変形行列
を得ることができます。getRotationMatrixの引数は普通の角度でOKです。ラジアンを使う必要もありません。
これらを使って上記スクリプトを書き換えると…
var matA = getTranslationMatrix(-100, -100);
var matB = getRotationMatrix(30);
var matC = getTranslationMatrix(100, 100);
var sel = app.activeDocument.selection;
for (var i = 0; i & lt; sel.length; i++) {
sel[i].transform(matA, true, true, true, true, 100, Transformation.DOCUMENTORIGIN);
sel[i].transform(matB, true, true, true, true, 100, Transformation.DOCUMENTORIGIN);
sel[i].transform(matC, true, true, true, true, 100, Transformation.DOCUMENTORIGIN);
}うーん、これでは何も改善してませんね。
点(x,y)を表すベクトルをrとして、
(-100,-100)移動の変形行列をA、原点を中心に30°回転の変形行列をB、(+100,+100)移動の変形行列をCとしたとき、
rを(-100,-100)移動した点は
Ar
rを(-100,-100)移動して、原点を中心に30°回転した点は
B(Ar)
rを(-100,-100)移動して、原点を中心に30°回転して、さらに(+100,+100)移動した点は
C(B(Ar))
で表せます。
そして、行列の掛け算はなんと、結合則が使えるのです!
すなわち、
C(B(Ar)) = (CBA)r
これは事前にCとBとAを掛け算した変形行列を求めておけば、変形1回で「(-100,-100)移動して、原点を中心に30°回転して、さらに(+100,+100)移動」したのと同じ状態にできる、ということです。
んで、イラレはその変形行列の掛け算にも関数を用意してくれています。concatenateMatrixというやつです。
var matA = getTranslationMatrix(-100, -100);
var matB = getRotationMatrix(30);
var matC = getTranslationMatrix(100, 100);
var matABC = concatenateMatrix(concatenateMatrix(matA, matB), matC);
var sel = app.activeDocument.selection;
for (var i = 0; i < sel.length; i++) {
sel[i].transform(matABC, true, true, true, true, 100, Transformation.DOCUMENTORIGIN);
}なんか上はごちゃごちゃしましたけど、forループがシンプルになったので今度こそできあがりでーす。
ちなみにconcatenateTranslationMatrixとかconcatenateRotationMatrixとか使うともう少し短く書くこともできます。詳しくはOMビューワとかこことか見てください。
おしモアイ
[ExtendScript]
ExtendScriptで使ってはいけないグローバル変数名
JavaScriptしっかり書くならグローバル変数は極力なくして、どうしてもグローバル変数が必要なときはできるだけ独特な名前を、となるのでしょうけど、まぁInDesignやイラレでちょっとしたスクリプト書くときに、いちいちそんなこと気にしたくありません。適当な変数名で、グローバルスコープにベタ書きしてしまいがちです。
しかしそういうとき、適当につけた変数名が思わぬバグを引き起こすことがあります。たとえばファイルパスの変数名にpathとか、何かを反転する関数名にreflectとか、つい使ってしまいそうですけど、これらはバグの元です。(関数の中のローカル変数で使うのは問題ありません)
この手のバグ、知識として知っとかないと原因の特定がすごく難しいので、この際まとめておきます。
ExtendScriptはJavaScriptの亜種なので、JavaScriptでグローバル変数名に使っちゃダメなもの、たとえばeval、alert等の組み込み関数の名前や予約語等は、もちろんExtendScriptでもダメです。
ここでは「普通のJavaScriptならOKだけどExtendScriptではダメなもの」を紹介します。
ただし、ExtendScript全体で共通のものと、InDesign・イラレ独自のものだけです。フォトショやAEにも独自のものがあると思いますが詳しくないので触れません。
アプリケーション独自のものには
アプリケーション独自のものはDocument、PageItem、TextFrameなど膨大にありますが、
最初が大文字の変数名を避ければいいので、ここでは列挙しないことにします。
すべてのオブジェクトが持つということは、グローバルオブジェクトも持っています。
そしてグローバル変数というのはグローバルオブジェクトのプロパティでもあります。
したがって、グローバル変数で「Object.prototypeのプロパティ名」を使おうとすると、グローバルオブジェクトがもともと持っているプロパティと競合してしまうので使ってはいけません。
ExtendScriptにあり、今のJavaScriptにはないものとして
(watch、unwatchは昔のJavaScriptにはあったらしい)
スクリプトの書き出しは、
みたいなので始まることが多いですが、これを
と書いても動くのです。
この謎仕様により、イラレスクリプトではappの持つプロパティ名をグローバル変数名に使えません。
appのプロパティ一覧(CS6)はこちらhttp://jongware.mit.edu/iljscs6html/iljscs6/pc_Application.html
うっかり使ってしまいそうなものとしては、
※Photoshopでも同じ問題があるようです。(お~まちさんに教えていただきました)
(ちなみに似たような謎仕様として、textRange.characterAttributes の characterAttributes も省略できます)
オワリ
しかしそういうとき、適当につけた変数名が思わぬバグを引き起こすことがあります。たとえばファイルパスの変数名にpathとか、何かを反転する関数名にreflectとか、つい使ってしまいそうですけど、これらはバグの元です。(関数の中のローカル変数で使うのは問題ありません)
この手のバグ、知識として知っとかないと原因の特定がすごく難しいので、この際まとめておきます。
ExtendScriptはJavaScriptの亜種なので、JavaScriptでグローバル変数名に使っちゃダメなもの、たとえばeval、alert等の組み込み関数の名前や予約語等は、もちろんExtendScriptでもダメです。
ここでは「普通のJavaScriptならOKだけどExtendScriptではダメなもの」を紹介します。
ただし、ExtendScript全体で共通のものと、InDesign・イラレ独自のものだけです。フォトショやAEにも独自のものがあると思いますが詳しくないので触れません。
1.アプリケーションオブジェクト
- app
2.ExtendScript独自の組み込み関数名
ExtendScript共通のものとしてはXML絡みの- isXMLName
- setDefaultXMLNamespace
アプリケーション独自のものには
- exit(InDesignのみ)
- resolve(InDesignのみ)
3.各種コンストラクタ名
ExtendScript共通のものはUnitValue、Reflection、BridgeTalkなど、アプリケーション独自のものはDocument、PageItem、TextFrameなど膨大にありますが、
最初が大文字の変数名を避ければいいので、ここでは列挙しないことにします。
4.Object.prototypeのプロパティ名
Object.prototypeのプロパティというのは、すべてのオブジェクトが共通して持っているプロパティのことです。すべてのオブジェクトが持つということは、グローバルオブジェクトも持っています。
そしてグローバル変数というのはグローバルオブジェクトのプロパティでもあります。
したがって、グローバル変数で「Object.prototypeのプロパティ名」を使おうとすると、グローバルオブジェクトがもともと持っているプロパティと競合してしまうので使ってはいけません。
ExtendScriptにあり、今のJavaScriptにはないものとして
- reflect
- watch
- unwatch
(watch、unwatchは昔のJavaScriptにはあったらしい)
5.appのプロパティ名(イラレ、フォトショのみ)
イラレスクリプトでは、なぜかapp.が省略できます。スクリプトの書き出しは、
var doc=app.activeDocument;みたいなので始まることが多いですが、これを
var doc=activeDocument;と書いても動くのです。
この謎仕様により、イラレスクリプトではappの持つプロパティ名をグローバル変数名に使えません。
appのプロパティ一覧(CS6)はこちらhttp://jongware.mit.edu/iljscs6html/iljscs6/pc_Application.html
うっかり使ってしまいそうなものとしては、
- name
- path
- version
※Photoshopでも同じ問題があるようです。(お~まちさんに教えていただきました)
(ちなみに似たような謎仕様として、textRange.characterAttributes の characterAttributes も省略できます)
オワリ
[ExtendScript]
比較演算がなんかおかしいExtendScript
ExtendScriptでは
がtrueになるけど、変数を使って
とするとfalseになる(JavaScript的に正しいのはfalse)
っていう話をだいぶ前に書いたんですが(これの8番目)
他にもnullと==で比較した結果がおかしいものを見つけました。
0, "0", "" です。("0"はfalsyですらないのに…)
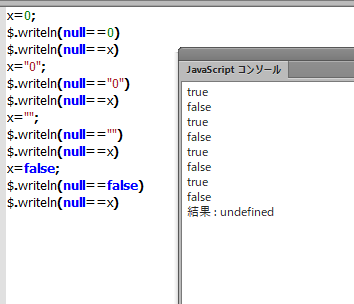
似たような現象はこんなのでも起きます。
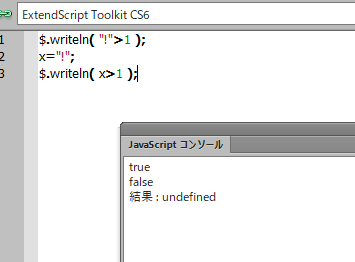
数値と文字列の比較では文字列側をNumberに変換するので、"!"はNaNになって、「NaNは比較演算子で何と比較してもfalseを返す」という性質があるので false になるはずなのですが、変数に入れずに直接比較すると true になってしまいます。変数がある場合は正しいです。
でー、変数があるかないかでなんでこんな違いが発生するのかなんですけど、
JSXBIN化を使ってみるとヒントめいたものが見えてきます。
これは「null==false;」をJSXBIN化した文字列
@JSXBIN@ES@2.0@MyBbyBn0ABJAnAFct0DzABByB
そしてこれは「true;」をJSXBIN化した文字列です。
@JSXBIN@ES@2.0@MyBbyBn0ABJAnAFct0DzABByB
完全に一致です。
これは比較演算だけでなく、「1+1」と「2」とかでも同じになります。
つまりはJSXBIN化(コンパイル)した時点で既に演算されてるのです。
変数のある演算は、実際にプログラムが動いてその行に行きつくまで結果がわからないけど、1+1とか0==nullみたいなプリミティブ値のリテラル同士の演算は最初から結果がわかってるので、高速化のためにもコンパイル時に演算しておこう、ということなんだと思います。
で、その演算が間違ってると。
ここまでは「値を直接演算するとおかしいけど、変数があれば正しい」というもので、実際のスクリプトで出てくるのはほぼ変数ありの演算でしょうから、まあ罠ではあるけどそんなに深刻なバグではありません。
次のは変数があろうとなかろうと、常におかしいやつです。
undefined < 任意の数
は、JavaScript的にはfalseになるのが正しいですが、ExtendScriptではtrueになります。
たとえばこんなコードでうっかり引数を入れ忘れて実行したらtrueが返ってきてしまいます。
ちなみに任意の数ってのは0とか100だけでなく、Infinityや-Infinityも含まれます。
「undefinedはマイナス無限大よりも小さい」ということになってしまうのです。
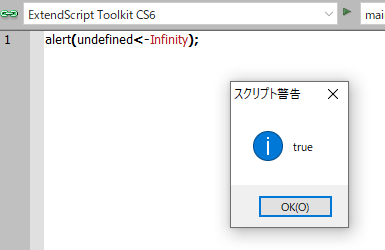
オワリ
false==null;がtrueになるけど、変数を使って
x=false;
x==null;とするとfalseになる(JavaScript的に正しいのはfalse)
っていう話をだいぶ前に書いたんですが(これの8番目)
他にもnullと==で比較した結果がおかしいものを見つけました。
0, "0", "" です。("0"はfalsyですらないのに…)
似たような現象はこんなのでも起きます。
数値と文字列の比較では文字列側をNumberに変換するので、"!"はNaNになって、「NaNは比較演算子で何と比較してもfalseを返す」という性質があるので false になるはずなのですが、変数に入れずに直接比較すると true になってしまいます。変数がある場合は正しいです。
でー、変数があるかないかでなんでこんな違いが発生するのかなんですけど、
JSXBIN化を使ってみるとヒントめいたものが見えてきます。
これは「null==false;」をJSXBIN化した文字列
@JSXBIN@ES@2.0@MyBbyBn0ABJAnAFct0DzABByB
そしてこれは「true;」をJSXBIN化した文字列です。
@JSXBIN@ES@2.0@MyBbyBn0ABJAnAFct0DzABByB
完全に一致です。
これは比較演算だけでなく、「1+1」と「2」とかでも同じになります。
つまりはJSXBIN化(コンパイル)した時点で既に演算されてるのです。
変数のある演算は、実際にプログラムが動いてその行に行きつくまで結果がわからないけど、1+1とか0==nullみたいなプリミティブ値のリテラル同士の演算は最初から結果がわかってるので、高速化のためにもコンパイル時に演算しておこう、ということなんだと思います。
で、その演算が間違ってると。
ここまでは「値を直接演算するとおかしいけど、変数があれば正しい」というもので、実際のスクリプトで出てくるのはほぼ変数ありの演算でしょうから、まあ罠ではあるけどそんなに深刻なバグではありません。
次のは変数があろうとなかろうと、常におかしいやつです。
undefined < 任意の数
は、JavaScript的にはfalseになるのが正しいですが、ExtendScriptではtrueになります。
たとえばこんなコードでうっかり引数を入れ忘れて実行したらtrueが返ってきてしまいます。
function f(x){
return x<0;
}
f();ちなみに任意の数ってのは0とか100だけでなく、Infinityや-Infinityも含まれます。
「undefinedはマイナス無限大よりも小さい」ということになってしまうのです。
オワリ
プロフィール
kawamoto_α
(あるふぁ(仮))
InDesignで新聞組版のようなことをしています。
ツイッタ
※ブラウザによっては当ブログからDLしたzipファイルが拡張子なしになることがあるようですが、.zipを補って開いてください。
イラレ用トーンカーブスクリプト(¥1500)
クロソイド式角丸長方形スクリプト(¥500)
Illustrator用
InDesign用
イラレスクリプトをキーボードショートカットで実行するやつ(Win用)
最近の記事
(02/17)
(01/12)
(01/06)
(12/24)
(12/03)
(10/08)
(10/06)
(09/07)
(08/04)
(06/24)
