[イラレ]
イラレで放物線をパッと描く
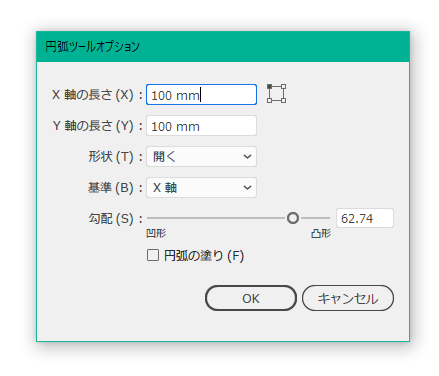
1.円弧ツールを選択して、ドキュメント上をクリックします
 2.「X軸の長さ」と「Y軸の長さ」を同じ値にして「勾配」を62.74にします
2.「X軸の長さ」と「Y軸の長さ」を同じ値にして「勾配」を62.74にします
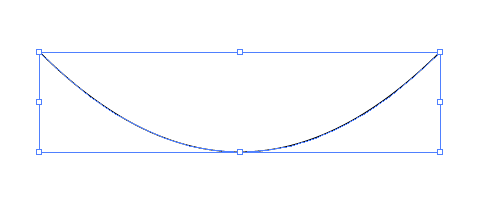
 3.できた曲線を45度回転してバウンディングボックスをリセットします
3.できた曲線を45度回転してバウンディングボックスをリセットします
オワリ
「放物線を水平または鉛直方向に変形しても放物線」「放物線は頂点と他の1点を決めれば一意に定まる」ことから、1つ放物線があれば変形によりどんな放物線でも作れることになります。
ためしに横6:縦9の比率に変形してみましょう。グリッドに重ねてみるとこの通り。(1,1)や(2,4)を通ってることがわかります。y=x^2のグラフですね。
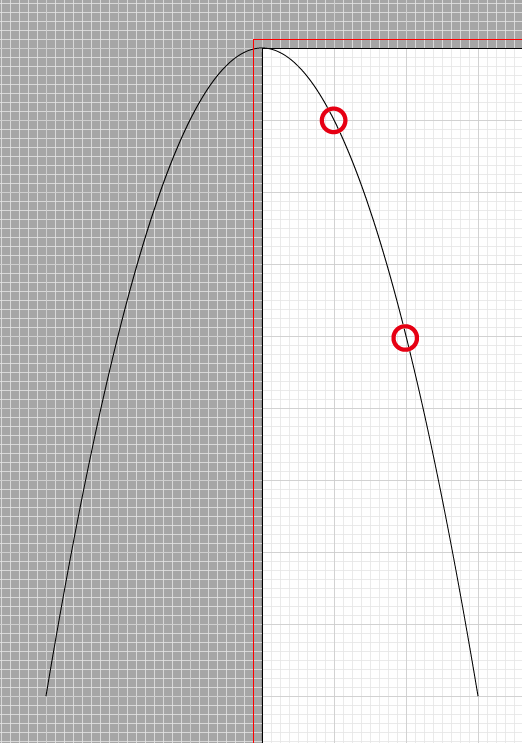
ちなみにイラレのパス(3次ベジェ曲線)で円弧は近似的なものしか描けませんが、放物線は正確に描けます。ただし円弧ツールのダイアログが小数第2位までしか有効じゃないので、ここに書いた方法ではせいぜい4桁程度の精度しかありません。
ここから追記
さすがに上記だけだと本当に放物線になるのか信じてもらえない感があるので円弧ツールについて補足してみます。
円弧ツールは1/4の円弧のような図形を描くツールなのですが、「勾配」っていうオプションがあって、これを動かすとアンカーポイントから出ているハンドルの長さが変化します。んで勾配0にするとハンドルの長さはゼロに、勾配100にすると「X軸の長さ」と同じになります。
となると、たとえば勾配50にしたら、ハンドルの長さはX軸の長さの50%になるのかなと思えますが、そうではありません。勾配とハンドルの長さは微妙に比例関係になっていなくて、50のときに正円の円弧に近くなるように調整されています。
グラフにするとこんな感じ。
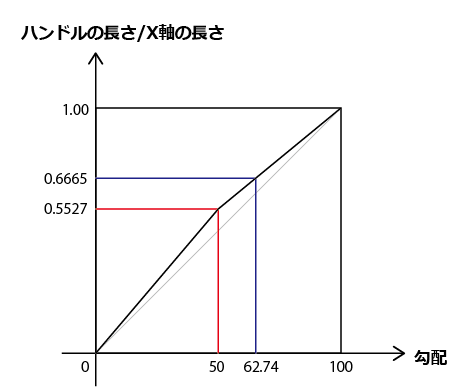
放物線になるのはハンドルの長さがX軸の長さの2/3倍のときなのですが、それにいちばん近くなるのが勾配=62.74のときであるということです。
結局なんで2/3で放物線になるのかの説明をすっとばしてるのであまり意味がなかった気がする
・双曲線(反比例のグラフ)の描き方
オワリ
「放物線を水平または鉛直方向に変形しても放物線」「放物線は頂点と他の1点を決めれば一意に定まる」ことから、1つ放物線があれば変形によりどんな放物線でも作れることになります。
ためしに横6:縦9の比率に変形してみましょう。グリッドに重ねてみるとこの通り。(1,1)や(2,4)を通ってることがわかります。y=x^2のグラフですね。
ちなみにイラレのパス(3次ベジェ曲線)で円弧は近似的なものしか描けませんが、放物線は正確に描けます。ただし円弧ツールのダイアログが小数第2位までしか有効じゃないので、ここに書いた方法ではせいぜい4桁程度の精度しかありません。
ここから追記
さすがに上記だけだと本当に放物線になるのか信じてもらえない感があるので円弧ツールについて補足してみます。
円弧ツールは1/4の円弧のような図形を描くツールなのですが、「勾配」っていうオプションがあって、これを動かすとアンカーポイントから出ているハンドルの長さが変化します。んで勾配0にするとハンドルの長さはゼロに、勾配100にすると「X軸の長さ」と同じになります。
となると、たとえば勾配50にしたら、ハンドルの長さはX軸の長さの50%になるのかなと思えますが、そうではありません。勾配とハンドルの長さは微妙に比例関係になっていなくて、50のときに正円の円弧に近くなるように調整されています。
グラフにするとこんな感じ。
放物線になるのはハンドルの長さがX軸の長さの2/3倍のときなのですが、それにいちばん近くなるのが勾配=62.74のときであるということです。
結局なんで2/3で放物線になるのかの説明をすっとばしてるのであまり意味がなかった気がする
関数の描き方シリーズ
・サインカーブの描き方・双曲線(反比例のグラフ)の描き方
PR
プロフィール
kawamoto_α
(あるふぁ(仮))
InDesignで新聞組版のようなことをしています。
ツイッタ
※ブラウザによっては当ブログからDLしたzipファイルが拡張子なしになることがあるようですが、.zipを補って開いてください。
イラレ用トーンカーブスクリプト(¥1500)
クロソイド式角丸長方形スクリプト(¥500)
Illustrator用
InDesign用
イラレスクリプトをキーボードショートカットで実行するやつ(Win用)
最近の記事
(02/17)
(01/12)
(01/06)
(12/24)
(12/03)
(10/08)
(10/06)
(09/07)
(08/04)
(06/24)
